Alexandre Billon (Université Charles-de-Gaulle - Lille 3), "Are infinite explanations self-explanatory?"
Erkenntnis, 2021
Why why why? Or how I tried to vindicate children's thirst for explanations

Kids know: adults’ explanations are disappointing, always.
Why did Grandpa have an accident? asks Jonas.
Because he was driving too fast.
But this answer is only really enlightening if he knows why Grandpa was going too fast.
Why was Grandpa going too fast?
I mention the fact that he drinks a little too much and disregards speed limits, but it goes on.
Why?
...
Why?
...
I usually tire before he does, and give up trying to explain the existence of the first hominids or the emergence of fish from the ocean. Other parents, perhaps less naturalistic than me, end up invoking God's will. They invariably get one,
But who created God?
When they begin to suspect that their lives aren't infinite and that they'll never get to the end of their questions, however, children get bored too. They grow up. They make up their minds. You always have to stop at one:
Because that's the way it is, and that's all there is to it.
Our explanations are disappointing and there's nothing we can do about it, period. The children know it.
The quest for a complete explanation and the metaphysicians' trilemma
There are, however, a handful of beings apart who grow up more or less normally, but don't give up their childish ambitions. Cosmologists, some theoretical physicists, and metaphysicians. The latter have produced a fascinating argument which is based on the principle (often called, after Leibniz, “principle of sufficient reason”) that everything must have an explanation, and that there must therefore be satisfactory explanations: "complete explanations" (that's the term they use) that don't arbitrarily stop at one "because that's the way it is".
But, they reason, if we start with an event E1 , say Grandpa's accident, and find an explanation E2 , and if we find an explanation E2 of E3, etc., and if we assume that everything does have an explanation, only three possibilities are open to us:
Our explanation continues like this to infinity: E1 is explained by E2 which is explained by ... which is explained by En , which is explained by En+1 , which is explained by ...
Our explanation bites its own tail, for example, E1 is explained by E2 which is explained by E3 which is itself explained by E1 !
Our explanation stops at something self-explanatory: for example, E1 is explained by E2 which is explained by E3 which is explained by E3 itself!
The cosmological argument for the existence of God
The first two options have almost always been rejected. Many philosophers deny that circular or infinite explanations can be true explanations. Others, more cautiously, admit that they are acceptable explanations, but deny that they can provide complete, entirely satisfactory explanations. Suppose, to take the case of infinite explanatory series on which I'm going to concentrate here, that E1 is explained by E2 which is explained by... which is explained by En , and so on. Each event Ei is indeed explained by the next, but the infinite series itself is not explained. This is the meaning of a famous argument by Leibniz, who imagines an infinite series of scribes, each copying the book of the next. Suppose the first scribe copied the Bible because the second had also copied the Bible, because, and so on. In this infinite series, the fact that any scribe copied the Bible is explained by the fact that he was copying the book of the next scribe who had himself copied the Bible... But that doesn't explain why they all copied the Bible rather than the Elements of Geometry. Each event is well explained by the next, but the totality of events is not, and our explanation is not complete.
From the incompleteness of infinite (or circular) explanations, many philosophers have concluded that there must be something absolutely fundamental that explains itself. Seeing nothing but God to explain itself and everything else, many have concluded that God must exist for us to have satisfactory explanations. This is known as the cosmological argument for the existence of God. It is as old as metaphysics itself.
More naturalistic philosophers, who regard the existence of God or even of a self-explanatory thing with suspicion, have tended to abandon childish metaphysical ambitions for a fully satisfying explanation. Explanations will always come up against the unexplained, and the best we can do is to ensure that this unexplained is not too strange, and does not clamor too insistently for an explanation that we won't be able to find for it.
Complete explanations without God or self-explanatory entities
In the article, “Are infinite explanations self-explanatory?” just published in Erkenntnis, I attempt to avenge those naturalist philosophers who have not given up their childish hopes of a complete explanation. More precisely, I show, against Leibniz, that infinite or circular explanations can be complete, and do better than theistic explanations.
My argument is based on a number of examples of infinite and complete explanations - I'll present one of them below - but I didn't arrive at these counter-examples by chance, and I can say something here about how I found them. I trained as an engineer before becoming a philosopher, and in the basic sciences, we almost never use the notions of explanations or causes. Instead, we substitute a notion that greatly clarifies these, that of functional dependence. By substituting this notion of functional dependence for that of explanation, we can easily realize what's wrong with Leibniz's argument, and understand that infinite or circular explanations can, in some cases, be complete. Below, I explain the idea of functional dependence and then present the key example of the article.
Functional dependence
In fundamental science, when one event E2 explains another E1 , the parameters that specify these two events are linked by mathematical equations that make it possible to deduce E1 from E2. Better than that, the parameters e1 specifying E1 functionally depend on the parameters e2 specifying E2: there's a mathematical function f such that e1 = f(e2).
Let's take a simple example. The event E2 "this ball is dropped h meters from the ground" explains the event E1 "when it hits the ground, it has velocity v". The speed of fall (which specifies the event E1) is related to the height at which the ball is released (which specifies the event E2) by the following equation, derived from Newton's laws:
(where g is a constant approximately equal to 9.81)
And the parameters v of the first event (E1 ) depend functionally on those (h) of the second (E2 ):
By replacing the vague notion of explanation by this much more precise notion of functional dependence, I found general conditions on the type of functional dependence between the events E1 , E2 , ..., En , ... so that we have an infinite or circular, but complete, explanatory series. In this article, however, I passed over these general conditions in silence, because I had not managed to find a mathematically elegant formulation for them, and I had neither the space nor the resources to relate this notion of functional dependence to classical philosophical theories of explanations. In particular, I was unaware that there is a very fruitful and perhaps now dominant theory of explanations based on an idea very close to that of functional dependence, the "structural equations account" (cf. e.g. Schaffer 2015). I have repaired these two shortcomings in an article recently submitted to another journal and currently under revision.
A counter-example to the idea that infinite explanations are always incomplete
I can now present the simplest of my counter-examples to the idea that infinite explanations are always incomplete, if not downright vicious (I'll ignore the case of circular explanations until the end of this post). This counter-example is inspired by Leibniz's series of scribes. It's based on the idea that if the entire series is considered unexplained, in this case, it's because it remains indeterminate: the fact that each scribe copies the book of the next leaves entirely open the content of the book they're copying. If we could find an example where, on the contrary, the fact that each Ei is explained by the following one Ei+1 fully determines the series of (Ei ), then we'd have a complete explanation.
Consider, instead of an infinite number of scribes, an infinite number of adjusters and a soft plastic stick of finite size. Like Leibniz's scribes, the adjusters all behave, always, in the same way. When a stick is passed to them, they adjust it so that its size approaches lm. More precisely, if the stick passed to them has a length l they stretch or compress it to produce (and pass on to the next adjuster) a stick of length
The size of the stick l1 that the first adjuster receives from the second is explained by the size l2 of the stick received by the second adjuster from the third, and we have
Similarly, the size l2 of the stick received by the second adjuster is explained by that l3 of the stick received by the third adjuster
, etc. We can show that
and if the series is infinite, then necessarily
Unlike the case of Leibniz's scribes, where each term of the series is explained by the next, but the series as a whole remains indeterminate and, it seems, unexplained, here we have a case where the explanations of each term by the next determine the series as a whole. I show in the article that this justifies the idea that the series as a whole is well explained and that we have a complete explanation.
Of course, this example is trivial. Stick adjusters don't exist, and if they did, they'd be a curiosity at best. Nonetheless, this example shows that explanations that go to infinity (philosophers speak of regression to infinity) are not always a problem. Better still, it shows that descent to infinity can be a real asset since it allows us to obtain a complete explanation that we wouldn't get with a finite series.
I also show in the article that infinite explanations cannot be ruled out in the name of modern physics and that they are already more common in science than we think. They thus provide serious competitors to theistic explanations of the world.
Finally, infinite and complete explanations can be very simple and elegant, satisfying the curiosity of children who don't believe in God - but who have studied a little mathematics.
This brings me to an important question that I don't address in the article: why didn't philosophers see that there could be infinite complete explanations? Arguably, it is because it takes a bit of rigor and mathematics to refine the vague notion of explanation in terms of functional determination and to realize that infinite explanations can be complete. And yet, for almost a century now, metaphysicians aiming for rigor have drawn far more inspiration from logic than from mathematics.
References
Billon, Alexandre (2021). Are infinite explanations self-explanatory? Erkenntnis 88 (5):1935-1954.
Schaffer, J. (2016) Grounding in the image of causation. Philos Stud 173, 49–100. https://doi.org/10.1007/s11098-014-0438-1








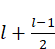




Perhaps this not-overly-mathematical philosopher is missing something. But if I were to seek a “complete explanation” of something (the logical possibility of which I doubt, just because it appears that we can always ask for more explanatory context), then I would require of the explanation of the “stick adjusters”, for instance, some explanation of where they came from, at least. That is, the set they comprise might be “self-explanatory”, in some technical (Pickwickian?) sense, but without an explanation for the existence of that overall set we appear to have a gaping hole in any normal sense of a “complete explanation”.