"Learning incommensurate concepts" - Hayley Clatterbuck (University of Wisconsin, Madison) & Hunter Gentry (University of Central Florida)

Synthese, 2025

Hayley Clatterbuck (L) & Hunter Gentry (R)

By Hayley Clatterbuck & Hunter Gentry

Is it possible to learn something genuinely new? Can you learn something you don’t already know? Famously, Jerry Fodor answered in the negative (1981). To learn a concept is to represent a hypothesis about the meaning of that concept and confirm it against the world. However, if you are successful, then you already knew the meaning of the concept! You can’t represent what you don’t already (in a sense) know. This problem has come to be known as the “learner’s paradox”.

In our paper, “Learning incommensurate concepts”, we attempt to dissolve the paradox and show that you can learn genuinely new concepts; concepts you don’t already know. To do so, we need to go beyond linguistic approaches to concepts and explore the interface between language and other kinds of representational formats.

We think that machine learning algorithms provide insights to help us answer the paradox. One thing that concepts do is group individuals together that are relevantly similar. We can think of dimensions of similarity as dimensions of a geometric space, and the overall similarity between two individuals as the distance between them in that similarity space. Learning processes can exploit geometric properties of the space to learn new concepts. We can learn that a cluster of individuals in a region of the space forms a category and can potentially learn a new concept that binds them together. More interestingly, we can learn something about the similarity space itself—about the relevant kinds of similarity in the world—from how individuals are located in that space. These latter learning processes can spur radical concept change, causing you to restructure the underlying similarity space that constitutes your conceptual landscape.

We focus on two main kinds of learning processes that can change one’s fundamental similarity space. First is dimension reduction. In many inference problems, you may start with more dimensions than you need to capture the underlying trends in the data, e.g. when your perceptual input is many-dimensional but the true signal is much simpler. Dimension reduction techniques (like Principal Component Analysis or PCA) allow us to find correlations in the data (features that “march together”) and to collapse correlated dimensions to a single dimension which characterizes the trend.

For example, imagine working on a factory assembly line. Your job is to record the weight and height of each object that passes by on the conveyor belt. You do this by plotting points in a two dimensional plane. On the x-axis is weight, the y-axis is height. You start off with a blank canvas—no data points recorded (you are brand new!). As you begin recording data points for the objects, you start to notice a pattern: the objects that are shorter weigh less and objects that are taller weigh more (see below).

Being the excellent, efficiency concerned employee that you are, you realize that you could more efficiently represent the data in a one-dimensional space by finding the line of greatest variance in the data, then plotting the points against that line (see below).

You’ve now reduced the number of dimensions you need. You’ve also learned a new concept, BULK, that was not represented before the learning process. Bulk is discoverable in the data, but it’s not explicitly represented. Indeed, it is an achievement to discover it!

We have illustrated dimension reduction with a very simple technique (PCA), but there are much more sophisticated dimension reductions that yield much more radical transformations to similarity spaces; indeed, we can see some DNNs, or parts of DNNs, as doing very radical dimension reduction (Buckner 2018). Two individuals that were very close together in the original similarity space may be very far apart in the new space (or vice versa). And since future learning groups individuals together by their distance, these transformations of the underlying space can significantly change future learning.

A second kind of learning process involves dimension expansion. In these cases, we are told that a group of individuals forms a category. However, these individuals do not form a coherent group in the original similarity space. If your data is telling you that there are two natural groupings here but you can’t make sense of these groupings with your original conceptual space, you must change your space to make sense of them. In effect, you ask, “if these are the natural kinds, what must the world be like?”. You can make sense of these groupings by adding dimensions to your space.

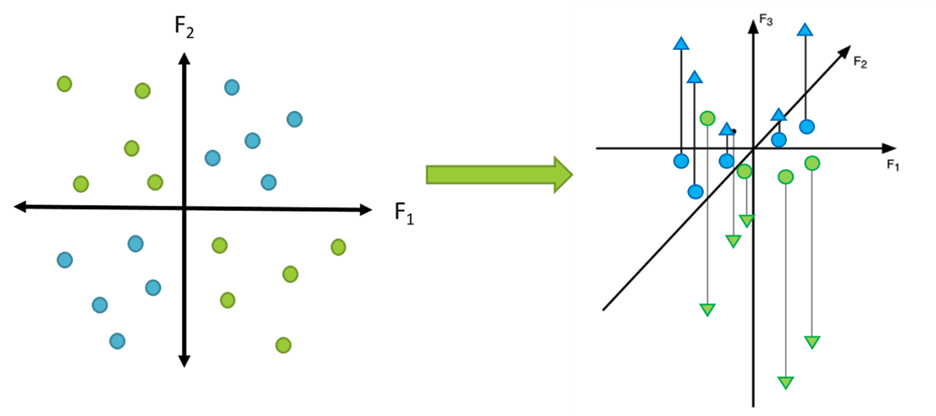
To be more specific, simple learning algorithms try to find simple geometric rules that distinguish between two categories. For example, we may try to find a line or hyperplane that divides them: everything on one side of the line belongs to group A and the other belongs to group B. Sometimes, though, this isn’t possible, as in the XOR plot below. You can get the blue dots and green dots to form neat, convex groupings by adding a third dimension, then pulling the blue dots up in that dimension and pulling the green dots down. Now, you can make a linear cut that neatly divides the two.

Left: 2-dimensional XOR plot. Right: projection of the data into a 3-dimensional space in which groups are linearly separable (reproduced from Harman and Kulkarni 2012, 43).

Once again, the dimension that is learned does not have to be explicitly represented prior to the learning process. You can find this dimension by trying to separate the data. This forms a hypothesis about a new kind of similarity in the world, the similarity that makes green things one kind and blue things another.

Dimension expansion provides a good model for thinking about how we learn new abstract concepts that are not easily definable in terms of simple perceptual regularities. Language, especially kind terms, provide the information about which things form real categories that can prompt us to start changing our spaces to make sense of them. As Sandra Waxman (1999) said, labels are invitations to form categories.

Here’s an example. Suppose you’re categorizing different kinds of animals, and you start with a simple similarity space where the dimensions are perceptual similarities. Mammals and fish will not form distinct, convex groupings in this space. The cats and dogs look similar to each other and quite unsimilar to any fish, but the dolphins look a lot like the sharks. Your teacher tells you that the dolphins belong to one group and sharks to another. In order to pull the dolphins apart from the sharks, you need to add an additional dimension of similarity (“produces milk” or “is a mammal” would both do). When you plot the animals in this new three-dimensional space, there is now a convex grouping that includes the dolphins and the cats and none of the fish.

We use simple learning processes to illustrate how new concepts can be learned that were not represented at the start and how some of these processes can yield radical changes to subsequent concept learning. We sketch out how this framework helps us think about cases of bootstrapping (Carey 2009) and other important kinds of concept learning.

We also show how it makes sense of how language interfaces with perceptual representations and how our thinking changes when it is supplemented with labels. This raises important questions about an old debate over the relation (or lack thereof) between language and thought. Is language merely a reflection of thought (Federenko et al. 2024)? Or does language play a more substantive role (Lupyan and Bergen 2016)? Our hypothesis supports the latter view.

References

Buckner, C. (2018). Empiricism without magic: Transformational abstraction in deep convolutional neural networks. Synthese, 195(12), 5339-5372.

Carey, Susan. (2009) The origins of concepts. Oxford University Press.

Fedorenko, E., Piantadosi, S. T., & Gibson, E. A. (2024). Language is primarily a tool for communication rather than thought. Nature, 630(8017), 575-586.

Fodor, J. A. (1981) The present status of the innateness controversy. In: Representations: Philosophical essays on the foundations of cognitive science [257–316]. MIT Press.

Harman, G., & Kulkarni, S. (2012) Reliable reasoning: Induction and statistical learning theory. MIT Press.

Lupyan, G., & Bergen, B. (2016). How language programs the mind. Topics in cognitive science, 8(2), 408-424.

Waxman, Sandra R. (1999) The dubbing ceremony revisited: Object naming and categorization in infancy, early childhood. In Folkbiology, eds. D. L. Medin & S. Atran [233–284]. MIT Press.